select *from ( select row_number()over(order by TempColmun) * from ( select top 开始的位置 0 as TempColmun,* from Student order by Id )tt)twhere rowNumber =开始的位置

4557: [JLoi2016]侦察守卫

Time Limit: 20 Sec  Memory Limit: 256 MB
Submit: 114  Solved: 70
[Submit][Status][Discuss]

Description

小R和B神正在玩一款游戏。这款游戏的地图由N个点和N-1条无向边组成，每条无向边连接两个点，且地图是连通的 。换句话说，游戏的地图是一棵有N个节点的树。游戏中有一种道具叫做侦查守卫，当一名玩家在一个点上放置侦 查守卫后，它可以监视这个点以及与这个点的距离在D以内的所有点。这里两个点之间的距离定义为它们在树上的 距离，也就是两个点之间唯一的简单路径上所经过边的条数。在一个点上放置侦查守卫需要付出一定的代价，在不 同点放置守卫的代价可能不同。现在小R知道了所有B神可能会出现的位置，请你计算监视所有这些位置的最小代价 。

Input

第一行包含两个正整数N和D，分别表示地图上的点数和侦查守卫的视野范围。约定地图上的点用1到N的整数编号。 第二行N个正整数，第i个正整数表示在编号为i的点放置侦查守卫的代价Wi。保证Wi≤1000。第三行一个正整数M， 表示B神可能出现的点的数量。保证M≤N。第四行M个正整数，分别表示每个B神可能出现的点的编号，从小到大不 重复地给出。接下来N–1行，每行包含两个正整数U,V，表示在编号为U的点和编号为V的点之间有一条无向边。N<= 500000,D<=20

Output

 仅一行一个整数，表示监视所有B神可能出现的点所需要的最小代价

Sample Input

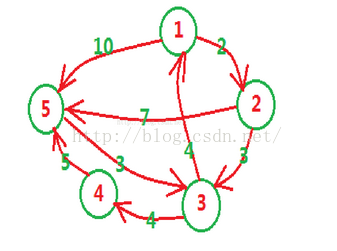
12 2
8 9 12 6 1 1 5 1 4 8 10 6
10
1 2 3 5 6 7 8 9 10 11
1 3
2 3
3 4
4 5
4 6
4 7
7 8
8 9
9 10
10 11
11 12

Sample Output

10

树形DP

f[i][j]表示i的子树中，最高覆盖到i向下第j层的最小花费。

g[i][j]表示i的子树全部覆盖，还能向上覆盖j层的最小花费。

转移比较麻烦，相关注释都写在代码里了。

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<cstring>
#include<algorithm>
#define F(i,j,n) for(int i=j;i<=n;i++)
#define D(i,j,n) for(int i=j;i>=n;i--)
#define ll long long
#define N 500005
#define inf 1000000000
using namespace std;
int n,m,d,cnt;
int w[N],head[N],f[N][25],g[N][25];
bool mark[N];
struct edge{int next,to;}e[N*2];
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
	while (ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
	return x*f;
}
inline void add_edge(int x,int y)
{
	e[++cnt]=(edge){head[x],y};head[x]=cnt;
	e[++cnt]=(edge){head[y],x};head[y]=cnt;
}
void dp(int x,int fa)
{
	if (mark[x]) f[x][0]=g[x][0]=w[x];//这个位置一定要放 
	F(i,1,d) g[x][i]=w[x];//初始状态是假设x位置放守卫，之后会可能被更新 
	g[x][d+1]=inf;//只用x子树中的点不可能向上覆盖d+1层，所以等于inf 
	for(int i=head[x];i;i=e[i].next)
	{
		int y=e[i].to;
		if (y==fa) continue;
		dp(y,x);
		D(j,d,0) g[x][j]=min(g[x][j]+f[y][j],g[y][j+1]+f[x][j+1]);//用y的子树中的守卫可能花费更少 
		D(j,d,0) g[x][j]=min(g[x][j],g[x][j+1]);//用g[x][j+1]来更新g[x][j] 
		f[x][0]=g[x][0];//这里相当于既不能向上也不能向下扩展 
		F(j,1,d+1) f[x][j]+=f[y][j-1];//直接加上就可以 
		F(j,1,d+1) f[x][j]=min(f[x][j-1],f[x][j]);//用f[x][j-1]来更新f[x][j] 
	}
}
int main()
{
	n=read();d=read();
	F(i,1,n) w[i]=read();
	m=read();
	F(i,1,m){int x=read();mark[x]=true;}
	F(i,1,n-1){int x=read(),y=read();add_edge(x,y);}
	dp(1,0);
	printf("%d\n",f[1][0]);
	return 0;
}

顶

0

踩

0