问题描述：

       数组是最为简单的数据结构之一，相同数据类型的元素按一定顺序排列的集合，也就是说把有限个类型相同的变量用一个名字命名，然后用编号区分他们的变量的集合，这个名字称为数组名，编号称为下标。组成数组的各个变量称为数组的分量，也称为数组的元素，有时也称为下标变量。数组的特性是占据一块连续的内存并按照顺序存储。因为这个特性，根据下标对于相应位置上元素的读/写操作能在O（1）的时间复杂度上完成，使用数组的时间效率是很高的，数组在哈希表，顺序表（C++的STL称其为Vector）等结构的应用是很广泛的，虽然数组也存在空间效率较低等方面的缺点，但是Vector，HashTable等数据结构在使用上应经针对各方面问题进行优化，主要目的是利用数组通过下标快速访问元素的特性。但数组虽为基础，数组方面的题型却是五花八门，各IT公司在考察前来应聘的应届生时，免不了从这种基础问题上开始问起，逐步细化，逐步加深。数组结构的确不难理解，但是要想完全驾驭数组，弄清数组知识点的方方面面，可以说也是不小的一项工作。

★数组的知识小点在这里就不一一赘述了，仅列举几道常见的考察数组特性的笔试题/面试题。

一：二维数组中查找某一个数

题目：在一个二维数组中，每一行都按照从左到右的递增顺序排序，每一列都按照从上到下递增的顺序排序。输入一个二维数组和一个整数，判断该数组中是否存在该数。

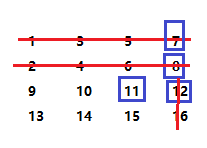
▲假设有这样一个数组，当看到这道题时我们的惯性思维是：假设输入的整数是11，如果用4与11进行比对，发现4小于11，说明下一比较的位置应该是下图蓝色方框以外区域的任意元素，这样不断重复该步骤，知道找到该元素；或者遍历完数组后依然未找到，说明不存在。

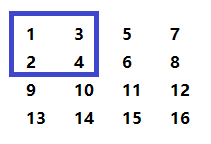
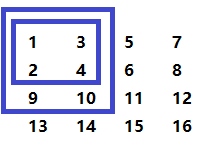
★上图的分析步骤虽然没有问题，但是要查找的数字相对于当前选取的位置可能在蓝色框的下方和右方出现，且这两个区域还存在重叠的情况，问题并未得到简化相反却变的复杂了，所以常常会使人感到陷入了僵局之中。其实解决该问题的方法很简单，同样以上图的数组为例，试图通过简单具体的例子找到普遍的规律。仍然假设要查找的数字为11。

①第一步：选取数组右上角的7与11进行比较，7比11小，所以肯定不会在7所在的行，所以该行可以剔除；

②第二步：剔除了第一行，现在数组的右上角元素为8，同样比较8和11，通过比较可以剔除8所在的行；

③第三步：此时右上角的元素为12，通过比较11小于12，所以肯定不会在元素12所在的列，因为12都比它大，何况12下面的元素，所以剔除元素12所在的列；

④第四步：此时右上角的元素恰好是11，所以通过比较找到了该元素。

代码：

bool Find(int* arr, int rows, int columns, int number)
{
	bool found = false;
	if (arr != NULL && rows > 0 && columns > 0)
	{
		int row = 0;
		int column = columns - 1;
		while (row < rows && column >= 0)
		{
			if (arr[row * columns + column] == number)//找到该元素
			{
				found = true;
				break;
			}
			else if (arr[row * columns + column] > number)//剔除列的情况，上例中的第三步的情况
			{
				--column;
			}
			else//剔除行的情况，上例中的第一及第二步情况
			{
				++row;
			}
		}
	}
	return found;
}

二：旋转数组中的最小数

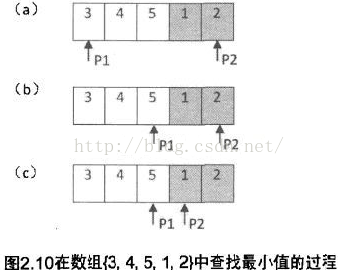
题目：把一个数组最开始的几个数字移到数组的末尾，称为数组的旋转，输入一个递增排序的数组的一个旋转，输出旋转数组的最小元素。例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转，该数组的最小值为1。

▲最简单的解法是从左到右遍历数组，找出最小的，但是时间复杂度是O(n)。 没有利用上排序的特性。一个递增的排序数组在旋转之后，也是部分有序的，前半部分递增，后半部分也是递增。所以可以考虑用二分查找的方法，其思想为指针start 指向左边数组的首元素，指针end 指向右边数组的末尾元素，指针middle = (start + end) / 2;在数组的开始和结束的位置放置两个指针，如果排除数组中有相同的数字的话，前半数组的部分比后半数组的部分大，此时，选择数组中间的元素，与左边的指针比较，如果比它大，证明左边的递增序列的长度超过整个序列的一半，最小的数字肯定在中间数字的右边部分，然后将左边的指针指向当前的中间的位置；同理，如果中间的数字啊比右边的指针指向的数字小，则最小的数字肯定在该数字的左边，然后将右边的指针指向这个位置。这样一来，查找的范围缩小一半，可以在O(lgn)的时间复杂度内找到最小的值。但是还有一些特例。

正常情况：
若data[middle] >= data[start]：说明最小值在middle之后，start = middle;
若data[middle] <= data[emd]:说明最小值在middle之前(包括middle) , end = middle; 
当end - start == 1，即start ，end相邻时：minNumber = data[end];
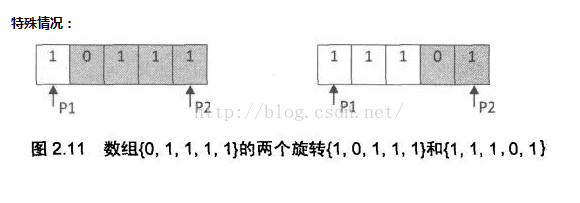
特殊情况：
旋转位数为0；递增数组未翻转；那么此时的最小值 minNumber = data[start]; {1,2,3,4,5}--》{1}
当大部分数组元素相等时：{2 ，1, 2, 2，2，2} , {2 , 2 , 2 , 2 , 1 , 2};
data[start] = data[middle] = data[end];可以在利用顺序遍历的思想；

代码：

//顺序遍历  
int MinInorder(int* data, int start, int end)
{
	int minNumber = data[start];
	for (int i = start + 1; i <= end; ++i)
	{
		if (minNumber > data[i])
			minNumber = data[i];
	}

	return minNumber;
}

int MinNumber(int* data, int length)
{
	if (data == NULL || length <= 0)
		return;

	int start = 0;
	int end = length - 1;
	//确保旋转位数为0，首部元素最小；  
	int middle = start;

	while (data[start] >= data[end])
	{
		//start和end相邻；  
		if (end - start == 1)
		{
			middle = end;
			break;
		}

		middle = (start + end) / 2;

		if (data[middle] >= data[start])  //最小值在后半部  
			start = middle;
		else if (data[middle] <= data[end]) //最小值在前半部  
			end = middle;

		//如果data[start]，data[middle]，data[middle]三者相等则进行顺序遍历  
		if (data[start] == data[middle] && data[middle] == data[end])
			return MinInorder(data, start, end);

	}

	return data[middle];
}

三：数组中出现次数超过一半的数字

题目：数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次，超过数组长度的一半，因此输出2。如果不存在则输出0。

▲分析：解法1：如果对这个数组排序，要找出出现次数超过数组长度一半的数字，这个数字就是长度为n的数组第n/2大的数字即中位数，可以用快速排序的方法找出任意第K大的数字 算法复杂度为O（n)。

             解法2：数组中有一个数字出现的次数超过数组长度的一半，也就是说它出现的次数比其它所有数字出现次数的总和还要多。因此我们可以遍历数组的时候，保存两个值，一个是数组中的数字，一个是次数。当我们遍历下一个数字时，如果这个数字与之前保存的数字不一样，则次数减1；若相同则次数加1， 如果次数为0则保存这个数字并将次数加1。由于要找的数字出现的次数比其它数字出现的次数之和还要多，因此要找的数字肯定是最后一次把次数设为1时对应的数字。 

代码-------->解法1：

int MoreThanHalfNum_2(int arr[], int len)
{
	if (CheckInvalidArray(arr, len))
	{
		return -1;
	}
	int result = arr[0];
	int times = 1;
	for (int i = 1; i < len; i++)
	{
		if (times == 0)
		{
			result = arr[i];
			times = 1;
		}
		else if (arr[i] == result)
		{
			times++;
		}
		else
		{
			times--;
		}
	}
	if (!CheckMoreThanHalf(arr, len, result))
	{
		return -1;
	}
	return result;
}



//检查数组是否合法  
bool CheckInvalidArray(int arr[], int len)
{
	isValid = false;
	if (arr == NULL || len <= 0)
	{
		isValid = true;
	}
	return isValid;
}


//检查num出现次数是否超过数组一半  
bool CheckMoreThanHalf(int arr[], int len, int num)
{
	int times = 0;
	for (int i = 0; i < len; i++)
	{
		if (arr[i] == num)
		{
			times++;
		}
	}
	bool MoreThanHalf = true;
	if (times * 2 <= len)
	{
		MoreThanHalf = false;
		isValid = true;
	}
	return MoreThanHalf;
}

代码--------->解法2：

bool CheckInvalidArray(int arr[], int len)
{
	isValid = false;
	if (arr == NULL || len <= 0)
	{
	<span style="white-space:pre">	</span>isValid = true;
	}
	return isValid;
}


//检查num出现次数是否超过数组一半  
bool CheckMoreThanHalf(int arr[], int len, int num)
{
	int times = 0;
	for (int i = 0; i < len; i++)
	{
		if (arr[i] == num)
		{
			times++;
		}
	}
	bool MoreThanHalf = true;
	if (times * 2 <= len)
	{
		MoreThanHalf = false;
		isValid = true;
	}
	return MoreThanHalf;
}

//先对数组进行排序，然后中间的那个数就是出现次数超过一半的数字(O(nLogn)
int partition(int arr[], int low, int high)
{
	int val = arr[low];
	while (low < high)
	{
		while (low < high && arr[high] >= val)
		{
			high--;
		}
		arr[low] = arr[high];
		while (low < high && arr[low] <= val)
		{
			low++;
		}
		arr[high] = arr[low];
	}
	arr[low] = val;
	return low;
}


//快排  
void QuickSort(int arr[], int low, int high)
{
	if (arr == NULL || low >= high)
	{
		return;
	}
	int index = partition(arr, low, high);
	QuickSort(arr, low, index - 1);
	QuickSort(arr, index + 1, high);
}


int MoreThanHalfNum(int arr[], int len)
{
	if (CheckInvalidArray(arr, len))
	{
		return -1;
	}
	QuickSort(arr, 0, len - 1);
	if (!CheckMoreThanHalf(arr, len, arr[len / 2]))
	{
		return -1;
	}
	return arr[len / 2];
}

顶

1

踩

0